Teoria de campo escalar φ 4 para separação de fases de partículas ativas

Teorias recentes prevêem a separação de fases entre partículas ativas orientacionalmente desordenadas, cuja velocidade de propulsão diminui rapidamente com a densidade. Modelos grosseiros deste processo mostram que a simetria de reversão do tempo (equilíbrio detalhado) é restaurada para estados uniformes, mas quebrada por termos de gradiente; portanto, a violação do equilíbrio detalhado está fortemente associada a fenômenos interfaciais. Para explorar a física genérica sutil resultante de tal acoplamento, apresentamos aqui o 'Modelo Ativo B'. Esta é uma teoria de campo escalar φ 4 (ou modelo de campo de fase) que viola minimamente o equilíbrio detalhado por meio de um termo de gradiente quadrado de ordem principal. Descobrimos que este termo adicional tem efeitos modestos na dinâmica de engrossamento, mas altera o diagrama de fase estática ao criar um salto na pressão (termodinâmica) através de interfaces planas. Ambos os resultados são surpreendentes, uma vez que os fenómenos interfaciais estão sempre fortemente implicados na dinâmica de engrossamento, mas são, em sistemas de equilíbrio detalhado, irrelevantes para o equilíbrio de fases.

Introdução

Muitas pesquisas recentes abordaram materiais ativos, cujas partículas constituintes violam a simetria microscópica de reversão de tempo (TRS) ao converter continuamente combustível em movimento.
Sistemas com ordem orientacional de médio ou longo alcance, como enxames de bactérias semelhantes a bastonetes 1 , podem então ser vistos como cristais líquidos ativos, que são descritos com sucesso pela adição de termos ativos mínimos às equações contínuas estabelecidas para a hidrodinâmica de cristais líquidos. As teorias de campo resultantes envolvem parâmetros de ordem vetorial ou tensorial que descrevem o estado local de ordem orientacional 2 , 3 .

No entanto, um paradigma alternativo importante aborda fases isotrópicas de partículas coloidais ativas (isto é, autopropelidas). Podem ser microrganismos naturais, como bactérias ou algas 3 , 4 , ou micronadadores sintéticos 5 , 6 , 7 , 8 , 9 . Em muitos desses casos, a dinâmica é descrita aproximadamente por ter um tempo de relaxamento fixo τ para a direção do movimento autopropelido, mas uma dependência não trivial da velocidade de propulsão υ ( ρ ) na densidade da partícula ρ . Se d ln ( υ ) / d ln ( ρ ) <−1, pode-se demonstrar que a separação de fases em estado estacionário surge através de um mecanismo de feedback positivo no qual uma desaceleração das partículas leva ao seu acúmulo e vice-versa 10 , 11 . Em sistemas biológicos, tal abrandamento pode surgir através de várias causas, tais como um acoplamento da resposta de detecção de quorum das bactérias à sua motilidade 4 , 12 . Para nadadores sintéticos, que são frequentemente modelados como 'partículas brownianas ativas' (ABPs), cuja direção de natação gira por difusão, uma diminuição efetiva em υ em alta densidade pode resultar de interações colisionais 13 , 14 .

Este cenário de separação de fases de partículas ativas está agora totalmente estabelecido em estudos de simulação 13 , 14 , 15 , 16 , 17 , 18 , e parcialmente confirmado por experimentos 19 , 20 . Isso não pode acontecer em sistemas com TRS microscópicos para os quais a acumulação em estado estacionário por desaceleração é proibida. Na verdade, o TRS do estado estacionário, também conhecido como "princípio do equilíbrio detalhado", garante que a densidade de equilíbrio é controlada apenas por forças conservadoras entre partículas (através da distribuição de Boltzmann) e não por quaisquer coeficientes cinéticos dependentes da densidade 10 , 21 . Por exemplo, numa suspensão isotérmica de partículas coloidais brownianas, a difusividade diminui fortemente em alta densidade, sem efeito no diagrama de fases. Em tais colóides "passivos", a separação de fases requer interações atraentes.

Para sistemas coloidais passivos, a cinética de separação de fases resultante é bem descrita por teorias de campo dinâmico envolvendo um campo de parâmetro de ordem escalar conservado φ , linearmente relacionado à densidade local de colóides. Simplificando a energia livre subjacente para um polinômio quártico em φ com termos de gradiente quadrado e assumindo dinâmica difusiva local, obtém-se então uma teoria chamada 'Modelo B'. Tais teorias de campo escalar φ 4 (ou modelos de campo de fase) têm desempenhado um papel fundamental na compreensão da separação de fases em sistemas com TRS 22 , 23. Isto se aplica particularmente quando os termos de ruído são negligenciados, criando um modelo de campo médio que captura com precisão a dinâmica de longo prazo da separação de fases, que é dominada pelo movimento determinístico de interfaces bem definidas. Nesse limite, o Modelo B torna-se a forma mais simples da equação de Cahn-Hilliard 24 , capturando um célebre resultado universal, L ~ t 1/3 , para a dependência do tamanho do domínio L no tempo t 25 .

Apesar da profunda distinção entre separação de fases ativa e passiva, a granulação grossa explícita da dinâmica ativa em grandes escalas estabelece um mapeamento parcial entre os dois casos. Este mapeamento foi encontrado primeiro para modelos de bactérias nadadoras com reorientações discretas 10 , mas posteriormente estendido para ABPs 11 . Na ordem zero em gradientes espaciais, o que equivale a considerar apenas sistemas de densidade uniforme, o mapeamento permite construir uma energia livre em massa cujas instabilidades são as do sistema ativo 10 , 11 . (A seguir, todas as grandezas termodinâmicas, como pressão e potencial químico global, referem-se àquelas calculadas neste mapeamento.) O equilíbrio detalhado, embora ausente microscopicamente, ressurge nesta ordem. Recentemente, no entanto, estudamos os termos do gradiente de ordem principal e descobrimos que eles quebravam o equilíbrio detalhado mais uma vez 14 . Isto cria uma nova classe de modelos em que a quebra do TRS está intimamente ligada à física das interfaces.

Esta característica distingue tais modelos de outros que abordam instabilidades difusivas do tipo Cahn-Hilliard em sistemas sem equilíbrio detalhado (ver, por exemplo, refs 26 , 27 , 28 , 29 , 30 ). Estes últimos abrangem muitos processos físicos, mas muitas vezes são demasiado complexos para que a sua física fundamental seja compreendida. Ao elucidar a física genérica da separação de fases de partículas ativas, é, portanto, importante focar no modelo mais simples da estrutura necessária.

Neste artigo, apresentamos e analisamos exatamente esse modelo. Para criar nosso novo modelo, adicionamos o termo de gradiente 'não integrável' mais simples (conforme definido abaixo) ao que de outra forma seria a teoria de campo padrão para separação de fases localmente difusiva, ou seja, Modelo B 22 , 23 . O termo gradiente escolhido quebra o equilíbrio detalhado no padrão, Modelo Passivo B, o que implica que o Modelo Ativo B resultante não pode ser derivado de qualquer funcional de energia livre.

Abaixo relatamos simulações de cinética de fase com o Modelo Ativo B, que ecoam resultados encontrados anteriormente usando um modelo contínuo mais elaborado inspirado em simulações de ABP 14 . Descobrimos que o termo não integrável não altera muito o destino dinâmico do sistema. Isto é notável, uma vez que a dinâmica de engrossamento é controlada pela tensão interfacial, que desaparece sem os termos do gradiente e, portanto, deve ser sensível à sua forma. Também apresenta um paradoxo quando confrontado com outro novo resultado: o Modelo Ativo B não admite nenhuma solução estática de parede de domínio conectando duas regiões em massa, cujo potencial químico μ 0 ≡d f 0 /d φ com a densidade de energia livre em massa f 0 leva o valor definido pela construção da tangente comum. (Conforme lembrado abaixo, esta construção é válida na coexistência, independente dos termos de gradiente, para todos os sistemas com equilíbrio detalhado.) Explicamos o resultado da 'tangente incomum' resultante em termos de um análogo induzido por atividade da pressão de Laplace que surge mesmo através de interfaces planas. . Este insight nos permite explicar por que a dinâmica de engrossamento ativo, a caminho da separação total de fases, permanece semelhante à do Modelo Passivo B tradicional.

Resultados

Modelo Ativo B

De acordo com os princípios descritos acima, adotamos a seguinte dinâmica para um campo de parâmetro de ordem escalar conservado φ ( r , t ) na posição r e no tempo t em d dimensões:

Todas as quantidades tornam-se adimensionais através do uso de "unidades naturais"; estes são υ (0) τ para comprimento e o tempo de relaxamento orientacional τ para tempo, onde υ (0) é a velocidade de natação de uma partícula isolada. A variável de composição φ está relacionada à densidade numérica ρ ( r , t ) de partículas ativas por uma transformação linear φ =(2 ρ − ρ H − ρ L )/( ρ H − ρ L ), onde ρ H e ρ L são as densidades de fases coexistentes de alta e baixa densidade, respectivamente, conforme calculadas, por exemplo, a partir de υ ( ρ ) pelos métodos das referências 10 , 11 .

Aqui a equação (1) expressa a conservação de φ , enquanto a equação (2) afirma que sua corrente média J – Λ é proporcional ao gradiente de um potencial químico fora de equilíbrio μ obedecendo à equação (3) com uma constante λ . Nossa nomenclatura para μ é autoexplicativa: mesmo além do equilíbrio, o potencial químico é a quantidade cujo gradiente causa a corrente média. O vetor Λ é um ruído branco gaussiano cuja variância consideramos constante. Isto segue a prática padrão no Modelo Passivo B, embora na realidade a variância seja dependente da densidade, conforme calculado explicitamente para partículas ativas na ref. 10 . O ruído é frequentemente negligenciado por completo nos estudos de separação de fases 31 e geralmente o ignoramos abaixo.

Na equação (3), μ = μ 0 + μ 1 é a soma das contribuições de volume e gradiente. A parte a granel é escolhida como a forma usual do Modelo Passivo B, μ 0 =− φ + φ 3 , de modo que na ordem zero em uma expansão gradiente, nosso Modelo Ativo B compartilha com sua contraparte passiva a densidade de energia livre a granel de um sistema simétrico φ 4 teoria de campo, f 0 =− φ 2 /2+ φ 4 /4. Observe que a separação de fases, impulsionada pelo termo linear negativo em μ 0 , pode surgir apenas da atividade, sem necessidade de interações atrativas. O termo gradiente é a soma de dois termos adicionais. A primeira é uma peça integrável ou 'passiva' , que pode ser escrita como uma derivada funcional de alguma energia livre ∫ f 1 d d r , enquanto a segunda é uma parte ativa , o que não pode.

Agora fazemos a escolha padrão do Modelo Passivo B, f 1 =( ∇ φ ) 2/2 , de modo que . No caso passivo, escolher a densidade total de energia livre f = f 0 + f 1 , em que f 0 é complementado pelo termo de gradiente quadrado mais simples f 1 =( ∇ φ ) 2/2 , captura todos os aspectos universais do física subjacente, ao mesmo tempo que permite uma análise muito mais simples da estrutura e dinâmica interfacial do que seria uma escolha mais realista de f . As mesmas vantagens valem para nosso Modelo Ativo B. Para o termo não integrável, escrevemos ; a constante λ é um parâmetro do modelo. Esta é a adição mais simples a μ , de segunda ordem em gradientes, que não pode ser derivada de uma energia livre ou de um funcional de Lyapunov. Observe que esta propriedade é a definição de 'não integrável' para os fins deste artigo.

A granulação grossa explícita da dinâmica dos ABPs 14 , 32 aponta para uma estrutura específica dos termos de gradiente na equação (3) e leva a um termo de gradiente μ 1 =− κ ( φ ) ∇ 2 φ com κ ( φ )=1 +2 λφ que combina exatamente nosso termo λ com uma parte integrável que corresponde a f 1 = κ ( φ )( ∇ φ ) 2 /2. Nas unidades do Modelo Ativo B, o parâmetro λ , cujo sinal pode ser absorvido pelo de φ se preferir, é então negativo e de ordem unitária para ABPs (ver Nota Suplementar 1 onde é dada uma expressão explícita para λ ). O mesmo se aplica às bactérias que correm e caem, cuja dinâmica é quase equivalente 11 . Em ambos os casos, λ é definido principalmente pela forma da função υ ( ρ ), parametrizando o decaimento com a densidade da velocidade média de natação. Enquanto isso, parâmetros dimensionados como υ (0) e τ servem para definir fatores de conversão entre unidades do Modelo Ativo B e unidades de laboratório.

A substituição da forma de granulação grossa derivada de f 1 por uma com constante κ = 1 é uma prática padrão para o Modelo Passivo B, assim como se substitui uma f 0 de granulação grossa complicada pela forma padrão f 0 =− φ 2 /2+ φ4 / 4. (É assim que o Modelo Passivo B descreve uma ampla gama de modelos microscópicos.) No Modelo Ativo B, fazemos exatamente as mesmas simplificações para todos os termos integráveis, enquanto capturamos a nova física com o termo mínimo de quebra de TRS de ordem principal. . Além disso, mostramos na Nota Suplementar 1 que todas as possíveis contribuições de corrente de ordem principal, até terceira ordem em ∇ e segunda ordem em φ , são dadas combinando alguma escolha de densidade de energia livre f com esta escolha de .

O termo não integrável do Modelo Ativo B lembra um pouco aquele que surge na célebre equação de Kardar-Parisi-Zhang para difusão interfacial não linear 33 , que foi construída em bases minimalistas semelhantes, e também apoiada pelo contato direto com argumentos microscópicos para exemplos específicos.

Dinâmica do Modelo Ativo B

Exploramos a dinâmica do Modelo Ativo B numericamente para supressores simétricos (∫ φ d d r = 0) e assimétricos (∫ φ d d r ≠0) nos quais um estado inicial uniforme, com leve ruído, é evoluído pelas equações ( 1, 2, 3). Nossos resultados estão de acordo com um estudo anterior, que mostrou que a não integrabilidade leva, no máximo, a mudanças quantitativas, mas não qualitativas, na dinâmica de engrossamento 14 . Isto se aplica aqui também, tendo em mente que o termo λ também quebra a simetria φ →− φ de uma têmpera simétrica. (Em duas dimensões, isso resulta em uma gota em vez de uma estrutura de domínio bicontínua, assemelhando-se a uma extinção ligeiramente assimétrica.) A Figura 1 mostra instantâneos de estruturas de domínio em evolução para λ = 0, −1, −2, com campos médios de parâmetros de ordem iniciais correspondentes para uma têmpera simétrica (com densidade média φ 0 ≡< φ ( r ,0)>=0) e uma têmpera diluída ( φ 0 =−0,4). O caso de uma têmpera densa ( φ 0 =+0,4) não é muito diferente, exceto por uma taxa de engrossamento ligeiramente mais lenta. Conforme observado acima, os resultados para λ positivo podem ser gerados invertendo o sinal de φ . Dados correspondentes para | λ |≤0,1 não é mostrado, mas está muito próximo do caso λ =0.

A Figura 2 mostra a evolução temporal do tamanho do domínio característico L ( t )~ t α para vários λ e φ 0 em duas e três dimensões. Aqui vemos algumas evidências de uma tendência descendente com o aumento | λ | do expoente α do valor conhecido α =1/3 do Modelo Passivo B 31 . Distinguir um deslocamento assintótico real em α de um cruzamento influenciado por λ exigiria um estudo computacional exaustivo 34 , que deixamos para trabalhos futuros. Observe, no entanto, que uma mudança de expoente descendente semelhante foi relatada na ref. 14 , mas descobriu-se que é reproduzível em um modelo integrável de Cahn-Hilliard, embora com um f 0 não polinomial , para o qual o poder assintótico de 1/3 é garantido. Isto sugere um cenário de cruzamento no qual todos os termos de gradiente, sejam ativos ou passivos, fundem-se gradualmente em uma tensão interfacial efetiva que leva ao engrossamento t 1/3 , uma vez que L é muito maior que a largura interfacial. Mais argumentos para este resultado são apresentados abaixo e nas Notas Suplementares 2 e 3 . Embora o caso de uma lei de escala t 1/3 assintótica padrão seja convincente, nosso próximo resultado mostra que o termo λ no Modelo Ativo B certamente não é representável apenas por uma mudança na tensão interfacial, uma vez que isso não teria efeito no equilíbrio de fases.

Resultados numéricos (pontos com barras de erro) e ajustes de mínimos quadrados (linhas retas) para a escala de comprimento de domínio L ( t ) para diferentes λ e densidade média φ 0 em duas e três dimensões: ( a ) d =2, φ 0 =0; ( b ) d =2, φ 0 =−0,4; ( c ) d =3, φ 0 =0; ( d ) d =3, φ 0 =−0,4. Observe a aparente tendência descendente com o aumento | λ | do expoente α do valor bem conhecido α = 1/3 do Modelo Passivo B. As barras de erro denotam o sd dos dados numéricos das curvas de ajuste correspondentes. A definição de L ( t ) é dada na seção Métodos.

Falha na construção da tangente comum

No Modelo Passivo B ( λ =0), a separação de fases em massa é caracterizada por duas fases estáticas coexistentes de extensão infinita que são separadas por uma interface planar. Essas fases em massa têm densidades φ → −1 e φ →1 para | z |→∞, respectivamente, onde z é uma coordenada perpendicular à interface. As densidades das fases coexistentes são definidas pela construção da tangente comum em f 0 ( φ ), conforme explicado detalhadamente abaixo, e implicam μ 0 =0 para | z |→∞. Além disso, as densidades constantes para | z |→∞ implica μ 1 =0 e, portanto, μ =0 em ambas as fases principais.

À primeira vista, espera-se que a construção da tangente comum ainda seja possível para λ finito , porque a contribuição ativa para o potencial químico de não-equilíbrio, , desaparece em ambas as fases a granel, e a própria construção se preocupa apenas com a densidade de energia livre a granel f 0 ( φ ) e não sobre tensão interfacial. Esta visão, no entanto, está errada porque a construção pressupõe implicitamente a integrabilidade, isto é, a existência de uma estrutura de energia livre em todos os lugares, incluindo quaisquer termos de gradiente. Na verdade, provamos aqui que não existe solução semelhante em μ =0 para o Modelo Ativo B, o que significa que a construção da tangente comum falha sempre que λ ≠0.

Em vez disso, para μ 0 =0 encontramos apenas soluções que descrevem fases espacialmente periódicas (lamelares). À primeira vista, estas descobertas sugerem que a separação de microfases, em vez da coexistência de fases em massa, pode ser o destino genérico do Modelo Ativo B. Isto é, por exemplo, o que acontece quando o Modelo Passivo B é acoplado a uma forma de atividade um pouco diferente, nomeadamente crescimento logístico da população 15 . Isto também é sugerido por vários experimentos em que partículas ativas formam aglomerados cujo tamanho aparentemente permanece finito em tempos longos 9 , 35 , 36 . Tal resultado seria, no entanto, paradoxal, dada a nossa descoberta numérica de desmixagem em massa em vez de separação de microfases no Modelo Ativo B. Para resolver este paradoxo, mostramos abaixo que existe uma interface planar entre estados totalmente separados por fases, mas suas densidades aparentes não são dados por uma construção tangente comum em f 0 .

Para provar isso, procuramos um estado totalmente separado por fases com uma interface planar e aproveitamos suas duas invariâncias translacionais para reduzir o problema a uma dimensão espacial. Para a solução estática necessária do Modelo Ativo B, isso significa φ = φ ( z ) onde z é uma coordenada normal à interface. Para descrever a separação estática de fases em massa, a corrente na equação (2) (com Λ = 0 ), especificamente seu componente z J z , deve desaparecer. (Assumimos que uma corrente uniforme é excluída pelas condições de contorno no infinito.) Isso requer que μ seja constante. Vamos primeiro tentar encontrar o seu valor seguindo o raciocínio usual de equilíbrio. A constante μ requer igualdade dos termos do potencial químico global μ 0 =d f 0 /d φ e também das pressões termodinâmicas globais P = φμ 0 – f 0 nas duas fases. (Lembre-se de que em sistemas fora de equilíbrio não existe uma relação geral entre a pressão termodinâmica assim definida e a pressão mecânica; voltaremos a este ponto abaixo.) Juntas, estas condições implicam que uma tangente comum pode ser traçada à curva f 0 ( φ ) nas duas densidades coexistentes. Como f 0 é simétrico, isso implica μ →0 para | z |→∞, de modo que por este argumento o potencial químico de não equilíbrio μ , que difere de μ 0 apenas nas regiões interfaciais, é zero em todos os lugares. O perfil de densidade estática φ ( z ) é então dado por

Ao renomear z e φ de acordo com ( z → t , φ → x ), esta equação para o perfil de densidade φ ( z ) pode ser mapeada na equação de movimento para a trajetória x ( t ) de uma partícula newtoniana de massa unitária em um potencial invertido simétrico U ( x )=− f 0 ( x ) sob a influência de uma força dependente da velocidade que é invariante sob reversão do tempo. A equação de movimento resultante é

Isso torna o cálculo do perfil de densidade φ ( z ) o mesmo problema que encontrar a trajetória x ( t ) de uma partícula newtoniana no potencial U ( x ) com uma força dependente da velocidade decorrente do termo λ . No caso passivo ( λ = 0), este mapeamento de Newton é um procedimento padrão (ver ref. 37 e referências nela), cujos detalhes relembramos na seção de Métodos. Em resumo, a solução domínio-parede é descrita por uma partícula que sai de um dos dois máximos em U ( x ) com velocidade infinitesimal, viaja através do vale no potencial invertido e então pára no outro máximo.

Diante desse quadro, consideremos o efeito de λ ≠0, ou seja, Modelo Ativo B. Isso cria uma força dependente da velocidade na equação (5), , que possui o mesmo sinal ao longo da trajetória. Por causa disso, se a partícula newtoniana começar muito perto do topo do primeiro máximo de U ( x ), isto é, se partirmos de um grande domínio de volume próximo à densidade aparente φ 1 =±1, a partícula também não chegue ao topo do outro máximo ou ele ultrapassará. O primeiro fornece oscilações periódicas entre a coordenada inicial x 1 e o ponto de viragem x 2 , que descrevem fisicamente a separação de microfases, enquanto o último fornece uma explosão não física. No caso da separação de microfases, a partícula newtoniana refaz seus passos a partir do ponto de viragem x 2 , que está finitamente abaixo do segundo pico, e recupera exatamente a energia cinética que perdeu para a força dependente da velocidade durante a primeira metade do ciclo. Portanto, ele chega exatamente a x 1 onde começou, praticamente para ali, criando outro grande domínio de φ 1 , antes de dar meia-volta e iniciar o ciclo novamente. Durante este movimento periódico, a partícula visita apenas brevemente os picos pares, criando um microdomínio da fase φ 2 cuja largura é da ordem da largura interfacial. Para tornar o domínio da segunda fase ainda mais amplo, o termo dependente da velocidade deve ser tornado exponencialmente pequeno (isto é, esses domínios têm uma largura que varia como −log| λ |). Somente isso permitirá que a partícula se aproxime do topo do outro máximo.

Se a partícula newtoniana, por outro lado, começa muito próximo do topo do segundo máximo de U ( x ), isto é, se se inicia com um domínio muito grande da segunda fase, e λ tem o sinal que impede a partícula de ultrapassar quando começa no primeiro máximo, o termo λ fornece energia à partícula para que ela agora ultrapasse. Estes argumentos confirmam que para λ ≠0 e μ =0, a separação estática da fase em massa é impossível.

Podem ser previstas três resoluções. Ou deixa de haver uma solução estática do Modelo Ativo B, ou as soluções que descrevem a separação de microfases tornam-se estáveis ​​ou μ é diferente de zero e a construção da tangente comum falha. Mostramos a seguir que a última destas resoluções se aplica.

A incomum construção tangente

Generalizamos agora a discussão da seção anterior para permitir um potencial químico de não-equilíbrio diferente de zero μ ≠0 obedecendo à equação (3). Mostramos que para o Modelo Ativo B, uma solução com uma interface planar entre duas fases coexistentes estáticas existe, mas é deslocada para um valor diferente de zero μ = μ b , de modo que as densidades coexistentes não sejam φ =±1. Também derivamos o potencial químico de não-equilíbrio resultante na coexistência da fase em massa μ b como uma função do parâmetro λ .

Para μ ≠0 a equação (4) para o perfil de densidade φ ( z ) torna-se

e a equação newtoniana correspondente é a equação (5) com o potencial agora assimétrico U ( x )= μx − f 0 ( x ). Definimos um valor crítico de | μ |= μ c tal que, sempre que | μ |< μ c , o potencial U ( x ) tem dois máximos nas posições e , com e um mínimo entre eles. Quando μ ≠0 as alturas dos dois máximos de U ( x ) são diferentes, e o sinal de μ decide qual máximo é menor. Em | μ |= μ c o mínimo e o máximo inferior se fundem em um ponto de sela, e como | µ | aumenta além do valor crítico μ c , resta apenas um único máximo. (Encontramos μ c =3 −1/2 –3 −3/2 ≈0,38.) Observe que μ c também pode ser definido como a inclinação máxima com a qual duas tangentes paralelas distintas podem ser desenhadas em f 0 ( φ ) (ver Figura 3 ). Esta inclinação máxima surge quando uma dessas tangentes passa pelo ponto de inflexão de f 0 ( φ ), também conhecido como ponto espinodal.

μ é igual nas fases coexistentes, e as pressões termodinâmicas P 1 e P 2 em cada fase são as interceptações negativas no eixo vertical. Aqui φ 1 e φ 2 são as densidades das duas fases coexistentes e Δ P λ = P 2 – P 1 é a diferença de pressão. Este gráfico mostra a construção para λ →∞, onde μ 0 ( φ 1 )= μ c

Devido a essas propriedades do potencial U ( x ) = μx − f 0 ( x ), para uma partícula newtoniana com a equação de movimento dada na equação (5), existem três tipos diferentes de movimento possíveis: (i) um movimento periódico movimento oscilatório entre dois pontos de viragem x 1 e x 2 com descrição da separação de microfases, (ii) o caso limite não periódico e que corresponde à separação de fases em massa e (iii) soluções divergentes correspondentes a perfis de densidade não físicos. Como existe apenas um máximo para | μ |≥ μ c , a separação de microfases e a separação de fases em massa são possíveis apenas para | μ |< μ c . Para | μ |≥ μ c , por outro lado, não existe solução física para o perfil de densidade estática φ ( z ).

A seguir, consideramos a situação | μ |< μ c e trate o aparecimento de separação de fases em massa como um caso limite especial de separação de microfases. A distribuição de densidade φ ( z ) para separação de fases em massa é uma solução especial da equação (6) ou equivalentemente da equação (5) com U ( x ) = μx − f 0 ( x ) para um valor apropriado μ = μ b do não -potencial químico de equilíbrio, que depende do parâmetro λ . A equação (5) com U ( x )= μx − f 0 ( x ) é uma equação diferencial ordinária não linear autônoma (EDO) de segunda ordem que não pode ser resolvida analiticamente. A função μ b ( λ ), entretanto, pode ser derivada desta equação mesmo sem resolvê-la. O procedimento é detalhado na seção Métodos e fornece um resultado analítico de 4/15 para a inclinação de μ b ( λ ) em λ = 0, bem como uma função implícita para μ b ( λ ), que é plotada na Fig. .

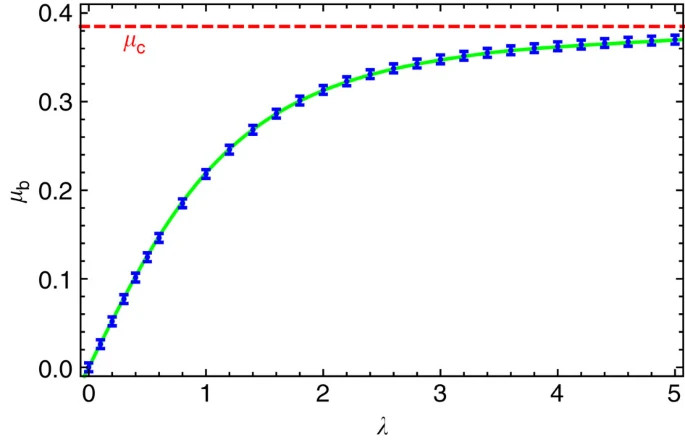
Resultado analítico (linha contínua) e resultados numéricos obtidos de simulações utilizando o Modelo Ativo B (pontos com barras de erro que denotam o erro de discretização estimado) para μ b ( λ ). Para λ →∞, a função μ b ( λ ) tende assintoticamente a μ c =3 −1/2 –3 −3/2 (linha tracejada). Apenas λ positivo é mostrado, uma vez que μ b ( λ ) tem a propriedade de simetria μ b (− λ )=− μ b ( λ ).

Com um gasto computacional muito maior, a função μ b ( λ ) também pode ser determinada a partir de simulações que resolvem a equação dinâmica (1) do Modelo Ativo B evoluindo até que um perfil interfacial de estado estacionário seja alcançado. Os resultados de tais simulações também são mostrados na Fig . A função μ b ( λ ) é zero para λ =0, aumenta monotonicamente para λ >0, e aproxima-se assintoticamente do valor crítico limite μ b (∞)= μ c para λ →∞. Usando a função μ b ( λ ), as densidades coexistentes φ 1 = φ (−∞) e φ 2 = φ (∞) são dadas pela menor e maior solução de U ′( φ )=0.

Os argumentos acima demonstram que soluções que descrevem a separação de fases estática existem para todos os valores de λ , mas são deslocadas para μ = μ b ≠0 e envolvem densidades coexistentes φ ≠±1. Outras soluções estáticas que descrevem, por exemplo, a separação de microfases lamelares, também existem, mas geralmente não são o resultado da resolução numérica da equação (1). Tais estados são genericamente instáveis ​​ao mesmo mecanismo de amadurecimento de Ostwald que no caso passivo (ver seção Métodos); isso é confirmado na Nota Complementar 3 para o caso de gotículas em dimensões superiores.

A coexistência de fase em massa no Modelo Ativo B é, portanto, governada por uma construção de 'tangente incomum' na qual as tangentes a f 0 ( φ ) são paralelas, mas deslocadas uma da outra (ver Fig. 3 ). Definindo como de costume a pressão termodinâmica aparente por P = φμ 0 − f 0 , o deslocamento vertical induzido por λ é identificado como uma diferença de pressão Δ P λ entre as fases aparentes coexistentes. A construção da tangente comum iguala μ 0 e P nestas fases; sua falha é, portanto, atribuível a um salto induzido por λ na pressão termodinâmica através da interface planar que os separa. Esta é uma consequência muito interessante e um tanto inesperada da atividade e da resultante quebra do equilíbrio detalhado nas regiões interfaciais.

A pressão ativa compete com a pressão de Laplace

O salto de pressão ativo Δ P λ não tem contrapartida direta em sistemas passivos. No entanto, para uma gota passiva com raio R a tensão interfacial γ (onde no Modelo Passivo B 34 ) cria um salto de pressão de Laplace Δ P L =( d −1) γ / R através da interface. Na Nota Complementar 2 , estabelecemos que para a ordem inicial em R grande (isto é, pequeno | λ |), existe uma solução estática μ = 0 para uma gota de raio na qual as pressões ativa e de Laplace são iguais e opostas; a tangência comum é assim restaurada. Isto pode acontecer apenas para uma das duas possíveis disposições de fases internas e externas, definidas pelo sinal de λ . Este resultado mostra que o salto de pressão induzido pela atividade Δ P λ tem, dentro do nosso mapeamento da separação de fases ativa para passiva, o mesmo status 'termodinâmico' que a pressão de Laplace.

A existência destas soluções de gotículas estáticas levanta mais uma vez a possibilidade de separação de microfases. Por exemplo, pode-se imaginar um estado de gotículas, cada uma com raio R *, incorporadas em uma fase contínua a zero μ . Se estável, tal fase pode explicar vários experimentos que mostram a formação de pequenos aglomerados finitos em bactérias e partículas coloidais ativas artificiais 9 , 35 , 36 . (Por motivos dimensionais, .) No entanto, isto contradiria os números relatados acima. Resolvemos isso observando que mesmo a solução de gota única é instável, conforme mostrado na Nota Complementar 2 . A instabilidade parece não ser fundamentalmente diferente da clássica de uma gotícula de fluido finita em equilíbrio instável com seu vapor (ver Figura 1 Complementar ). De fato, no Modelo Passivo B, existe um valor estacionário do raio da gota R 0 para μ > 0, mas este é um ponto fixo instável que separa o encolhimento do estado de crescimento da gota. Além disso, como mostrado quantitativamente na Nota Complementar 3 , a pressão ativa Δ P λ compensa a relação entre μ e o tamanho das gotículas, mas não pode impedir o engrossamento de um conjunto de gotículas pelo amadurecimento de Ostwald, no qual as pequenas evaporam e as grandes crescem ( veja a Figura 2 Complementar ). Este raciocínio aponta novamente firmemente para a lei de crescimento difusivo usual L ~ t 1/3 , que vale para a dinâmica do tipo Ostwald em morfologias de gotículas e bicontínuas 25 , e explica em grande parte a notável semelhança entre a separação de fases ativa e passiva. Também explica porque, no caso ativo, a separação de microfases não é o ponto final genérico da dinâmica; através do amadurecimento de Ostwald, o engrossamento prossegue indefinidamente. Os desvios de α = 1/3 encontrados numericamente são, nesta visão, quase certamente efeitos transitórios ou cruzados.

Pressão mecânica versus pressão termodinâmica

Em trabalhos futuros generalizaremos este estudo para permitir o acoplamento de um campo escalar ativo a um fluxo de solvente que conserva o momento. Lá apresentaremos uma contraparte ativa do 'Modelo H', que descreve tal acoplamento para sistemas passivos 22 , 23 . Isto levanta uma questão intrigante relativa à natureza da pressão, que definimos neste artigo como P = φμ 0 − f para coincidir com a definição termodinâmica padrão. Em sistemas passivos, isto é obviamente igual à pressão mecânica definida como uma força por unidade de área em um limite, ou através da parte diagonal do tensor de tensão. Assim, por exemplo, o salto de pressão de Laplace através de uma interface curva pode ser medido diretamente por uma sonda mecânica num sistema passivo.

Contudo, a equivalência da pressão mecânica e termodinâmica em tal sistema decorre, em última análise, do fato de que as mesmas forças interpartículas determinam tanto a mecânica quanto a termodinâmica. Em contraste, para partículas ativas, mesmo a parte integrável da energia livre não tem uma ligação simples com as forças interpartículas: em vez disso, codifica os efeitos da densidade na autopropulsão através do mapeamento da ref. 10 . Isto significa que a quantidade P encontrada através desse mapeamento geralmente não pode ser vista como uma pressão mecânica real. Isto não é surpreendente para um sistema longe do equilíbrio; na verdade, as pressões mecânicas e termodinâmicas diferem mesmo em sistemas bastante próximos do equilíbrio, como fluidos em fluxo. O salto de pressão ativo através de uma interface plana não poderia, portanto, ser medido com um manômetro, mas ainda é um salto de pressão no sentido termodinâmico de que P = φμ − f tem valores diferentes nas duas fases principais. Para uma interface curva, exatamente as mesmas observações se aplicam à contribuição da pressão de Laplace, sempre que a própria separação de fases e, portanto, a tensão interfacial resultante, é impulsionada pela atividade. Na verdade, a própria tensão interfacial impulsionada pela atividade não é detectável com um tensiômetro; seu significado decorre de sua capacidade de conduzir um fluxo difusivo de partículas ativas por meio do potencial químico fora do equilíbrio que aparece na equação (2).

Ao acoplar o sistema ativo a um solvente conservador de momento através da equação de Navier-Stokes, é a pressão mecânica que entra, não a termodinâmica. Como abordaremos em detalhes em outro lugar, na prática isso significa que um Modelo Ativo H deve combinar a dinâmica difusiva do Modelo Ativo B desenvolvido aqui com uma explicação conceitualmente separada das forças mecânicas criadas pela autopropulsão.

Dito isto, se restringirmos a atenção à classe de sistemas onde a separação de fases em massa é causada apenas por atrações entre partículas, de modo que o único efeito da atividade fraca é criar um valor diferente de zero de λ , mesmo a pressão mecânica no duas fases em massa é então desigual. Isso ocorre porque os termos do gradiente controlados por λ desaparecem em massa: portanto, a termodinâmica de equilíbrio comum se mantém localmente, e a pressão mecânica e termodinâmica deve mais uma vez coincidir em cada fase de massa. A atividade representada por λ desempenha um papel direto apenas próximo à interface, onde cria a condição de tangente incomum. Isto obriga o sistema a desenvolver um salto de pressão mecânica real e fisicamente mensurável entre as fases, igual à nossa pressão ativa. Note-se que a nossa pressão activa não é apenas a pressão mecânica que um gás activo confinado exerce sobre uma parede de recipiente 38 e que resulta directamente do aumento da velocidade e da acumulação superficial de partículas activas em comparação com as passivas. Em contraste com a pressão de um gás activo, o nosso salto de pressão através da interface entre uma fase diluída e uma fase densa de partículas activas não é proporcional à densidade e a sua origem é mais subtil.

Discussão

Argumentamos que, quando nenhum solvente está presente, de modo que a dinâmica é difusiva, a física da separação de fases da partícula ativa é totalmente capturada pelo Modelo Ativo B. Isso combina uma energia livre em massa φ 4 com termos de gradiente passivo e ativo de forma mínima. . Ele representa uma classe intrigante de problemas que envolvem separação difusiva de fases em sistemas onde violações de equilíbrio detalhado são criadas principalmente por interfaces. A estrutura minimalista do Modelo Ativo B permite não apenas uma simulação eficiente, mas também a obtenção de diversos resultados analíticos. Isto explica por que tais violações do equilíbrio detalhado têm efeitos paradoxalmente pequenos na dinâmica de engrossamento, para a qual a física interfacial é geralmente dominante, mas grandes efeitos no diagrama de fases, para o qual tal física é, à primeira vista, irrelevante. Equações um tanto semelhantes foram usadas recentemente para estudar o crescimento de cristais em sub-resfriamento finito 29 , 30 e seleção de estado na reologia de bandas de cisalhamento 39 . Nestes casos, sabe-se que termos gradientes não integráveis ​​podem destruir a construção da tangente comum para a coexistência de fases 30 , 39 . No Modelo Ativo B, a física que substitui a tangência comum é simples e notável: a igualdade do potencial químico entre as fases é mantida, mas a atividade cria um análogo direto da pressão termodinâmica de Laplace operando através da interface entre as fases principais que, ao contrário de sua contraparte de equilíbrio , permanece finito mesmo para uma interface planar.

Nosso trabalho lança luz direta sobre como o termo não integrável no Modelo Ativo B leva a previsões físicas novas e não intuitivas para a separação de fases de partículas ativas. O papel desempenhado por este termo ativo pode ser melhor entendido em termos do mapeamento em massa bem estabelecido entre a separação de fases ativa e passiva, ampliado aqui para incluir uma tensão interfacial mais um salto de pressão interfacial que não tem contrapartida passiva. Nossos resultados são ainda mais poderosos e surpreendentes porque até agora não encontramos nenhuma rota convincente para obtê-los por meio de raciocínio qualitativo aplicado diretamente ao movimento de partículas ativas. É muito difícil para tal raciocínio capturar a estrutura incomum do problema, que envolve a restauração do TRS (ausente microscopicamente) na ordem zero em gradientes espaciais e sua perda novamente em ordem superior. Uma interpretação totalmente microscópica dos nossos resultados pode, portanto, permanecer indefinida.

Métodos

Análise numérica

Para resolver numericamente o Modelo Ativo B, foi aplicado um esquema de diferenças finitas com condições de contorno periódicas. A distribuição espacial inicial do campo de parâmetros de ordem φ foi aleatória para os cálculos numéricos cujos resultados são mostrados nas Figuras 1 e 2 e uma função degrau (com φ = −1 para 64≤ z ≤192 e φ =1 caso contrário) para o resultados mostrados na Figura 4 . Tanto para simulações em duas quanto em três dimensões espaciais, o tamanho do passo de tempo foi Δ t =0,001, enquanto o tamanho do passo espacial foi Δ z =0,5 para duas dimensões e Δ z =1 para três dimensões. O tamanho da rede foi principalmente 256 × 256 para duas dimensões, com exceção de 256 × 50 para os cálculos numéricos correspondentes à Fig. 4 e 128 × 128 × 128 para três dimensões. Finalmente, a escala de comprimento de domínio L ( t ) na Fig. 2 foi calculada a partir do inverso do primeiro momento do fator de estrutura médio esférico S ( k , t ) 34 :

O fator de estrutura médio esférico é definido como

onde k =|| k || é o módulo do vetor de onda k , φ ( k , t ) é a transformada espacial de Fourier do campo de parâmetros de ordem φ ( r , t ) e denota uma média sobre uma camada no espaço k em k fixo .

Mapeamento de Newton

Aqui resumimos o mapeamento de Newton para o caso passivo onde λ =0 (ver Fig. 5 para um esboço). O potencial invertido U ( x )=− f 0 ( x ) tem dois máximos de igual altura em x =±1 com um mínimo entre eles. Para x <−1 e x >1 cai para menos infinito. Observe que a posição inicial x 1 = x (−∞) da partícula newtoniana com a equação de movimento (5) corresponde à densidade φ 1 = φ (−∞) da primeira fase global. A partícula newtoniana pode partir do repouso em um dos três domínios qualitativamente diferentes: (i) −1< x 1 <1, (ii) x 1 ε{−1,1} e (iii) x 1 <−1 ou x 1 >1. No caso (i) a partícula newtoniana oscila indefinidamente entre sua posição inicial x 1 e um ponto de inflexão na posição − x 1 . Para a distribuição de densidade φ ( z ) isso descreve um estado lamelar correspondente à separação de microfases. (Este estado pode ser visto em uma dimensão como uma série de gotículas, cada uma com tamanho e separação exatamente iguais.) Tal estado é instável (em qualquer dimensão) a pequenas variações de densidade, fazendo com que gotículas grandes cresçam às custas das pequenas. Este é o processo de Ostwald discutido mais detalhadamente na Nota Suplementar 3 .

Calcular o perfil de densidade φ ( z ) de um sistema com densidade de energia livre f 0 ( φ ) é o mesmo problema que encontrar a trajetória x ( t ) de uma partícula newtoniana no potencial externo U ( x )=− f 0 ( x ). Este esboço mostra a separação de fases em massa no Modelo Passivo B para λ =0 e d =1 como exemplo.

Por outro lado, no caso mais particular (ii) a partícula newtoniana parte do repouso infinitamente abaixo de um pico do potencial U ( x ), onde paira um longo tempo antes de começar a se mover, dispara para o outro lado e depois vem descansar infinitamente abaixo do outro pico. Isso pode ser feito em qualquer direção e fornece a solução familiar de parede de domínio que descreve a separação de fases em massa. Finalmente, no caso (iii) a partícula newtoniana acelera indefinidamente em direção a x =−∞ ou x =∞. Isto corresponde a uma solução divergente e não física da equação (4), que é de qualquer forma descartada pelas condições de contorno. Impondo φ ( z )=±1 em | z |→∞ seleciona o perfil interfacial em massa como a única solução estática estável, não uniforme do Modelo Passivo B.

Determinação da condição de coexistência

Para encontrar a função μ b ( λ ), primeiro reduzimos a ordem da equação (5) com U ( x )= μx − f 0 ( x ). A substituição o transforma em uma EDO não autônoma e não linear de primeira ordem. Uma outra substituição não invertível w ( x )= ν 2 ( x ) então leva à EDO linear de primeira ordem

Esta equação descreve a velocidade quadrada w ( x ) de uma partícula newtoniana, com a equação do movimento (5), em função da posição da partícula x . A equação (9) é muito mais simples que a EDO (5) com U ( x )= μx − f 0 ( x ) e pode ser resolvida analiticamente como

com o valor inicial w 0 = w ( x 0 ) na posição inicial x 0 = x (0), e o polinômio g λ ( x )=6+12 λx +4 λ 2 (3 x 2 −1)+8 λ 3 (− μ − x + x 3 ).

Com a ajuda da equação (10) a condição para separação de microfases pode ser escrita da seguinte forma: existem duas posições x 1 e x 2 com de modo que w ( x 1 )= w ( x 2 )=0. Esta condição é equivalente a h λ ( x 1 )= h λ ( x 2 ) com h λ ( x )= g λ ( x ) e −2 λx . A separação de fases em massa como um caso limite de separação de microfases aparece para e . A condição para separação de fases em massa pode, portanto, ser escrita como

Observe que o último termo em g λ ( x ) e, portanto, também em h λ ( x ) desaparece para . A condição (11) depende apenas de μ , que denotamos como μ b no caso de separação de fases em massa, e λ . Isso significa que a separação de fases em massa requer uma relação entre μ b e λ descrita por uma função μ b ( λ ).

Para (o que também implica ; observe que μ b =0 para λ =0) a função μ b ( λ ) pode ser encontrada a partir da equação implícita (11) expandindo esta última em λ e μ b . A solução perturbativa resultante da equação (11) é dada por

Além disso, a propriedade μ b (− λ )=− μ b ( λ ) segue da equação (11), de modo que não há termos de ordem par na equação (12).

Informações adicionais

Como citar este artigo: Wittkowski, R. et al. Teoria de campo escalar φ 4 para separação de fases de partículas ativas. Nat. Comum. 5:4351 doi: 10.1038/ncomms5351 (2014).

Fonte: https://www.nature.com/articles/ncomms5351