Usando ondas para medir o mundo: uma nova maneira de rastrear o fluxo de informações

Uma equipe de físicos descobriu que ondas eletromagnéticas espalhadas por um objeto contêm informações detalhadas e definidas localmente sobre as propriedades desse objeto. Essas informações, quantificadas por um conceito chamado informação de Fisher, fluem pelo espaço de uma forma análoga à forma como a energia flui em campos eletromagnéticos.

Em nossas vidas diárias, estamos cercados por ondas. Das ondas sonoras que carregam nossas vozes às ondas eletromagnéticas que alimentam nossos dispositivos sem fio, as ondas são fundamentais para como interagimos e entendemos nosso mundo. Cientistas e engenheiros há muito tempo usam ondas para explorar e medir tudo, desde as profundezas do oceano até a composição de estrelas distantes. Agora, um estudo inovador revelou uma nova maneira de entender como essas ondas carregam informações sobre os objetos que encontram.

Uma equipe de físicos descobriu que ondas eletromagnéticas espalhadas por um objeto contêm informações detalhadas e definidas localmente sobre as propriedades desse objeto. Essas informações, quantificadas por um conceito chamado informação de Fisher, fluem pelo espaço de uma forma análoga à forma como a energia flui em campos eletromagnéticos. Assim como o famoso vetor de Poynting descreve o fluxo de energia no eletromagnetismo, a equipe introduziu um novo "fluxo de informação de Fisher" que rastreia o fluxo de informação em campos de onda.

Esta pesquisa revolucionária publicada na Nature physics [1], abre novas possibilidades para entender e manipular ondas eletromagnéticas em várias aplicações, desde imagens médicas até telecomunicações. As implicações desta descoberta são de longo alcance e podem potencialmente revolucionar nossa abordagem às tecnologias baseadas em ondas.

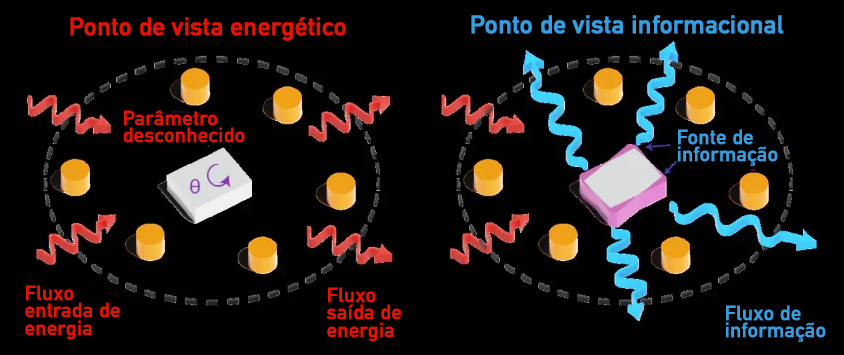
Fig. 1 Ilustração de medições de precisão em sistemas complexos. a, No ponto de vista da energia, uma região de espalhamento contendo dissipadores cilíndricos e retangulares é iluminada por luz coerente fornecendo um fluxo de energia de entrada (setas vermelhas de entrada). Um parâmetro θ (aqui a orientação angular do espalhador retangular) é estimado a partir do fluxo de energia de saída (setas vermelhas de saída). b, No ponto de vista de informação alternativa apresentado aqui, a informação de Fisher sobre um parâmetro específico θ é criada nas áreas que mudam com a variação de θ (áreas roxas nos cantos do retângulo) e a informação correspondente flui para fora do sistema (setas azuis de saída). Imagem e legenda retiradas de [1].

Essa nova compreensão do fluxo de informações é baseada em três características principais:

1. Definição local : O conteúdo de informação de Fisher pode ser atribuído a pontos específicos no espaço, assim como a densidade de energia em campos eletromagnéticos. Essa localização permite o mapeamento preciso da distribuição de informação dentro de um campo de onda.
2. Conservação : O fluxo de informações de Fisher segue uma equação de continuidade, semelhante à forma como a energia é conservada em ondas eletromagnéticas.
3. Mensurabilidade : Os pesquisadores demonstraram que esse fluxo de informações pode ser observado experimentalmente e quantificado usando experimentos de micro-ondas. Esse aspecto prático da descoberta abre caminho para aplicações no mundo real e estudos empíricos posteriores.

O conceito de informação de Fisher não é novo – ele tem sido usado em estatística e análise de dados por décadas. Em termos simples, a informação de Fisher quantifica o quanto um sinal nos diz sobre um parâmetro específico que estamos tentando medir. O que é revolucionário sobre esse novo trabalho é a percepção de que a informação de Fisher tem uma presença física em campos de onda, com sua própria densidade e padrões de fluxo.

Estudos anteriores analisaram como maximizar as informações de Fisher coletadas por detectores ou como moldar ondas de entrada para obter o máximo de informações de um sistema. No entanto, até agora, pouco se sabia sobre como as informações são criadas quando as ondas interagem com um objeto e como essas informações se propagam por ambientes complexos. Esta nova pesquisa abre a "caixa preta" do fluxo de informações entre um objeto alvo e nossos detectores.

Para visualizar esse conceito, imagine jogar uma pedra em um lago. As ondulações que se espalham carregam informações sobre o tamanho da pedra, o formato e o ponto onde ela atingiu a água. Agora, imagine ser capaz de ver não apenas as ondulações, mas também um "campo de informação" colorido que mostra exatamente onde e como a informação sobre a pedra está fluindo pela água. É essencialmente isso que essa nova teoria permite que os cientistas façam com ondas eletromagnéticas.

Os pesquisadores demonstraram sua teoria usando uma configuração experimental inteligente. Eles criaram um ambiente de dispersão complexo em um guia de ondas de micro-ondas – essencialmente uma caixa de metal que guia as micro-ondas. Dentro desta caixa, eles colocaram um alvo de metal móvel cercado por pequenos dispersores de Teflon. Ao medir precisamente os campos de micro-ondas ao redor do alvo conforme ele era movido ligeiramente, eles foram capazes de mapear o fluxo de informações de Fisher sobre a posição do alvo (Fig. 2).

Fig. 2 Fluxo de informações de Fisher em uma configuração de micro-ondas. a, Esboço da configuração experimental. Descrevemos os dispersores de Teflon como cilindros laranja e o dispersor de alvo metálico como um cubo cinza claro. As ondas são injetadas do lado direito, conforme indicado pela frente de onda azul claro. A área de medição de campo próximo é destacada em vermelho. b, Fluxo de informações de Fisher (setas azuis) para o caso em que o parâmetro estimado θ = x scat é a posição horizontal do objeto alvo cinza. c, Fluxo de informações de Fisher correspondente à sua posição vertical θ = y scat . A área ao redor do alvo é mostrada para o caso em que um estado de entrada é injetado (a 6,45 GHz), o que maximiza o FI na saída para o parâmetro θ fornecido. De acordo com nossas previsões, observa-se claramente que a informação de Fisher emerge das regiões roxas onde o índice de refração muda quando θ é perturbado. A linha tracejada indica onde a proximidade do objeto alvo proíbe medições de campo próximo, imagem e legenda tiradas de [1].

Veja como o experimento funcionou:

1. Micro-ondas foram injetadas no guia de ondas a partir de uma extremidade.
2. As ondas se espalharam pelo alvo e pelos objetos de Teflon ao redor.
3. Antenas sensíveis mediram o campo de micro-ondas resultante em muitos pontos ao redor do alvo.
4. O alvo foi movido ligeiramente e as medições foram repetidas.
5. Ao comparar os dois conjuntos de medições, os pesquisadores puderam calcular o fluxo de informações de Fisher em cada ponto.

Uma das descobertas mais surpreendentes deste trabalho é que o fluxo de energia e o fluxo de informação podem ser desacoplados (Fig. 3). Os pesquisadores demonstraram isso com uma simulação onde a maior parte da energia das ondas foi transmitida através de um sistema, mas quase todas as informações de Fisher fluíram na direção oposta. Isso tem aplicações potenciais em comunicação segura, onde você pode querer enviar informações em uma direção enquanto minimiza a energia detectável nessa mesma direção.

Para entender os detalhes técnicos de como as informações de Fisher se propagam, os pesquisadores derivaram uma equação de continuidade que descreve seu fluxo. Esta equação mostra que as informações de Fisher são criadas em "fontes" – áreas onde o campo eletromagnético muda quando o parâmetro de interesse (como a posição do alvo) é variado. As informações então fluem para longe dessas fontes, propagando-se para fora do sistema ou sendo reabsorvidas por "sumidouros", como áreas com dissipação de energia.

Fig. 3 Comparação da informação de Fisher e do fluxo de energia. Vetor de Poynting simulado (setas vermelhas em a) e fluxo de informação de Fisher (setas azuis em b) ao redor do dispersor alvo (índice de refração n = 1,44) em f = 11,8 GHz, ao injetar um estado incidente que maximiza a razão de informação de Fisher entre os canais de transmissão e reflexão. Com o parâmetro de estimativa θ de interesse aqui sendo o índice de refração do dispersor alvo, as fontes FI estão localizadas em toda a sua área (quadrado roxo em b). Tanto o dispersor alvo quanto a desordem (círculos laranja) têm um índice de refração de n = 1,44. Observamos que enquanto a maior parte da energia da onda é transmitida (96,3%) para a esquerda (veja a), quase toda a informação de Fisher (98,4%) está fluindo para a direção oposta (para a direita, veja b). Imagem e legendas retiradas de [1] .

A estrutura matemática desenvolvida neste estudo vai além de apenas situações estáticas. Os pesquisadores estenderam sua teoria ao domínio do tempo, mostrando como a informação de Fisher é gerada e armazenada em pacotes de ondas à medida que se propagam. Este aspecto temporal é crucial para entender como a informação se acumula em um sistema ao longo do tempo (Fig. 4).

Fig. 4 Conteúdo de informação de Fisher de um pacote de ondas. Um pacote de ondas unidimensional centralizado em torno de uma frequência ω se espalha em um dielétrico (retângulo cinza), cuja posição é o parâmetro de interesse. a, Envelope de densidade de energia (vermelho) nos tempos T = 2, 6,5, 10 (unidades arbitrárias). As setas pretas indicam a direção do movimento do pacote de ondas. b, Densidade de informação de Fisher (azul) nos mesmos tempos. A informação é criada nas fontes localizadas nos dois lados do dispersor (roxo). A maior parte da energia é transmitida, enquanto a informação flui apenas para o canal de reflexão. Imagem e legenda retiradas de [1].

Os pesquisadores também fizeram conexões com a mecânica quântica. Eles mostraram que a densidade de informação de Fisher integrada em sua estrutura corresponde à informação quântica de Fisher de estados de luz coerentes. Isso fornece uma base teórica sólida para seu trabalho e sugere que a estrutura poderia ser estendida a outros sistemas quânticos.

Ciência unificada em perspectiva

Embora essa pesquisa tenha se concentrado em ondas eletromagnéticas, os princípios subjacentes poderiam ser potencialmente aplicados a outros tipos de ondas, como ondas acústicas usadas em imagens de ultrassom ou ondas sísmicas usadas para estudar o interior da Terra. Essa ampla aplicabilidade torna o trabalho particularmente empolgante para campos que vão de imagens médicas a geofísica.

Esta descoberta preenche a lacuna entre conceitos matemáticos abstratos e a realidade física, fornecendo uma nova ferramenta para cientistas e engenheiros analisarem e manipularem fenômenos de ondas. Pode levar a melhorias em vários campos, como:

As implicações dessa nova compreensão do fluxo de informações são de longo alcance. Em campos como a optomecânica levitada, onde cientistas estão tentando resfriar partículas minúsculas para seu estado fundamental quântico, saber exatamente como as informações sobre a posição de uma partícula irradiam pode levar a esquemas de detecção mais eficientes. Em aplicações de imagem e sensoriamento, essa estrutura pode orientar o design de novos sistemas que maximizem a coleta de informações relevantes.

À medida que nosso mundo se torna cada vez mais dependente de medições precisas e transferência eficiente de informações, teorias como esta, que fornecem uma compreensão fundamental de como as informações se propagam por sistemas físicos, se tornarão cada vez mais cruciais. Este trabalho abre novas possibilidades para rastrear e projetar o fluxo de informações, mesmo em ambientes complexos e desordenados. É um passo significativo em nossa capacidade de usar ondas não apenas para ver o mundo, mas para realmente entendê-lo.

Referências:

[1] Hüpfl, J., Russo, F., Rachbauer, LM et al.
Equação de continuidade para o fluxo de informação de Fisher em espalhamento de ondas .
Nat. Phys. (2024). https://doi.org/10.1038/s41567-024-02519-8

https://spacefed.com/physics/using-waves-to-measure-the-world-a-new-way-to-track-information-flow/